ALTIMETRIA, NIVELACION DE TERRENOS Y PERFILES TOPOGRAFICOS

  Altimetría

La altimetría es la parte de la topografía que se encarga a medir las alturas, estudia los métodos y técnicas para la representación del relieve del terreno, así como para determinar y representar la altura; también llamada cota, de cada uno de los puntos, respecto de un plano de referencia.

Realiza la medición de las diferencias de nivel o de elevación entre los diferentes puntos del terreno, las cuales representan las distancias verticales medidas a partir de un plano horizontal de referencia. La determinación de las alturas o distancias verticales también se puede hacer a partir de las mediciones de las pendientes o grado de inclinación del terreno y de la distancia inclinada entre cada dos puntos. Como resultado se obtiene el esquema vertical.

La altimetría tiene por objeto representar la verdadera forma del terreno, es decir, no sólo su extensión, límites y obras que lo ocupan, sino también la forma se su relieve, haciendo para ello las operaciones necesarias. Este aspecto tiene mucha importancia para las aplicaciones de operaciones en el terreno, o sea, son aspectos de fundamental importancia dentro del contenido de la topografía para el ingeniero de la rama agropecuaria.

Nota: En planimetría no se consideraba la forma real del terreno, ya que solo se consideraba la proyección de la superficie sobre el plano horizontal.

Equipos y materiales usados

Los instrumentos utilizados en altimetría buscan perfección a la hora de medir alturas y elevaciones. El instrumento más importante en la materia es el Nivel, instrumento empleado en la nivelación por alturas, consiste en la determinación de la altura de los puntos del terreno, (en realidad de sus puntos característicos), sobre una superficie del nivel que se toma como superficie de comparación de nivel; esta superficie se puede elegir arbitrariamente y puede ser cualquiera, con la única condición de que todos los puntos de la superficie del terreno considerada estén situadas por encima de ellos.

También se usa una mira graduada, aunque para largas distancias pueden utilizarse un teodolito y un blanco. Este último método se denomina nivelación trigonométrica.

Conceptos Fundamentales

• Plano horizontal: Plano tangente a una superficie de nivel.
• Superficie de nivel: Superficie curva en donde cada punto es perpendicular a la dirección de la plomada; así el desnivel entre dos puntos es la distancia que existe entre la superficie de nivel de dichos puntos.
• Angulo vertical: Angulo entre dos líneas que se cortan en un plano vertical. En topografía se supone una de estas líneas de manera horizontal.
• Elevación o cota: distancia vertical medida desde un plano de referencia.
• Nivel medio del mar: altura media de la superficie de la mar media de la superficie del mar según todas las etapas de la marea en un periodo de 19 años.
• Banco de nivel (BM): Punto permanente en el terreno, natural o artificial, cuya elevación es conocida. El BM puede estar referenciado sobre nivel medio del mar (msnmm) o ser asumido para ciertos trabajos de campo. Existen BM de cota fija y que constituyen la red geodésica del país, construidos de concreto.
• Mojón (B.M): Materialización en el terreno de un punto plenamente definido. Esta materialización se hace en concreto y el punto se define por una puntilla (clavo) con marca centrada. De este tipo de puntos se conocen coordenadas amarradas a un sistema Geodésica y altura o cota sobre el nivel del mar.
• Estación: Punto perteneciente a una poligonal o circuito de nivelación del cual se requiere conocer la cota.
• Punto de Cambio: Punto intermedio de un circuito de nivelación y que sirve de apoyo al realizar un recorrido.
• BM Inicial: BM desde el cual arranca un circuito de nivelación y al cual se le conoce la cota o se asume al inicio de la nivelaci6n.
• BM Final: BM de 11egada al que se pretende encontrar la cota de desnivel. En muchas oportunidades tiene elevación conocida y permite controlar un circuito de nivelación.
• Contranivelación: Proceso de repetición de un circuito de nivelación desde un punto de llegada inicial, hasta el punto de partida. Este proceso no requiere pasar necesariamente por los puntos intermedios tomados inicialmente.
• Datum (nivel de referencia): Es un plano imaginario previamente definido. Uno de los más empleado es el nivel del mar.
• Circuito de nivelación: Es el proceso en el cual se hacen lecturas de V+, V-, VI' y se obtienen alturas de instrumento (A.I.) y cota.
• Circuito de nivelación cerrado: Es aquel circuito de nivelaeión en el cual se parte de un BM inicial o punto de partida y se regresa a él luego de realizar un recorrido.
• Circuito de nivelación abierto: Es aquel circuito de nivelación en el cual se parte de un BM inicial y se realiza un recorrido llegando a un BM final o punto final, diferente del BM inicial.
• Lectura de vista más (V+) o vista atrás: Es la lectura de mira realizada a un punto de cota conocida.
• Desnivel: Es la diferencia de altura 0 cota entre dos puntos.
• Cota: Es la altura entre un punto y un determinado nivel de reverencia.
• Altura de instrumento. (A.I):  Es la altura del plano horizontal en que se desplaza el instrumento de nivelaci6n con relaci6n a un punto de cota conocida.
• Lectura de vista intermedia (VI): Es una vista menos o lectura a un punto de detalle al que se requiere conocer la cota, el cual no interviene directamente en e1 proceso de nivelación.
• Lectura de vista menos (V-) o vista adelante: Es la lectura de mira realizada a un punto de cota desconocida.
• Nivelación Barométrica: se determina por medio de un Barómetro, puesto que la diferencia de altura entre dos puntos se puede medir aproximadamente de acuerdo con sus posiciones relativas bajo la superficie de la atmosfera, con relación al peso del aire, que se determina por el barómetro.
• Nivelación Trigonométrica o Indirecta (por pendientes): se puede determinar con una cinta y un clisímetro o bien, un teodolito, al basar sus resoluciones en un triángulo rectángulo situado en un plano vertical, por lo que se toman medidas de distancias horizontales y ángulos verticales.
• Nivelación Geométrica o Directa (por alturas): permitiendo la determinación directa de las alturas de diversos puntos, al medir las distancias verticales con referencia a una superficie de nivel, cuya altura ya es conocida.
• Perfil: Se llama perfil de un terreno a la representación geométrica del “corte” de su superficie por un plano vertical, trazado según una línea dada sobre dicho terreno.
• Rasantes: Las rasantes son las líneas que se proyectan sobre un perfil, ya sea para un canal, camino u obra similar, adoptando las “pendientes” que se estimen oportunas y quedando materializadas en el terreno por el fondo de las zanjas, cima del afirmado, etc., cuando hayan alcanzado las “cotas” señaladas y se ajusten a las alineaciones fijadas.
• El "trazado de rasantes”: Supone una serie de operaciones previas, que tienen por objeto reunir los datos necesarios para la formación del perfil del terreno sobre el que se han de proyectar las rasantes requeridas, operaciones ellas que vienen a constituir las “prácticas de nivelación”.
  
• Línea de nivel: Es toda línea perteneciente a una superficie de nivel y por consiguiente, normal a la dirección de la fuerza de gravedad en cada uno de los puntos.
• Nivel medio del mar: La superficie de los mares en clama tiene que ser siempre perpendicular a la gravedad, y, por tanto, es por definición una superficie de nivel. Esta condición posibilita que adoptando dicha superficie de nivel como superficie de cota 0 por todos los países, las elevaciones de la corteza terrestre pueden ser comparadas ente sí, cualquiera que sea el lugar en que se encuentren localizados. Ejemplo tenemos que el monte Everest en el Himalaya, tiene más de 6000m de alto que el pico Cuba. La altura del nivel medio del mar se mide con instrumentos llamados mareógrafos, instalados en aguas razonablemente tranquilas, en las proximidades de la costa. Para los trabajos geodésicos y topográficos, la determinación del nivel medio del mar la realizan instituciones especializadas de cada país y los mismos aparecen indicados en los mapas topográficos nacionales.
• Superficie de referencia arbitraria: Cuando se va a realizar un trabajo altimétrico en que se requiere conocer el desnivel relativo entre puntos característicos puede tomarse una superficie de comparación arbitraria, asignándole a un punto bien definido sobre el terreno o establecido con ese fin. Esto debe hacerse cuidando que la altura asignada al punto que vayan a levantarse quede por encima de la superficie de referencia, de manera que sus elevaciones sean positivas.
• Cota altimétrica: Son las elevaciones de los puntos con respecto a una superficie que se toma como referencia. Las superficies de referencia pueden ser el nivel del mar u otra superficie arbitraria, por eso es necesario distinguirla denominándose cotas altimétricas relativas a las elevaciones de los puntos sobre una superficie de comparación elegida arbitrariamente y cotas altimétricas absolutas o altitudes a las que se encuentran referidas al nivel medio del mar. En los trabajos técnicos se emplean más comúnmente la denominación de cotas absolutas, y en los trabajos y documentos de carácter científicos la denominación de altitudes.
• Punto de cota fija (PCF): Son aquellos puntos cuyas altitudes han sido determinadas y ajustadas, sirviendo estos valores como superficies de nivel de referencia para los diversos trabajos topográficos y su control. Estos puntos se encuentran distribuidos por todo el territorio nacional, en mayor o menor número, en dependencia del grado de desarrollo e importancia técnica-económica de cada zona, constituyendo lo que se denomina redes de apoyo y control altimétrico.
• Plano horizontal: Es el plano normal a la dirección de la fuerza de gravedad en ese punto, por lo tanto, es tangente a la superficie de nivel que pasa por dicho punto. En topografía técnica, el plano horizontal y la superficie de nivel correspondiente pueden considerarse coincidentes dentro de las distancias a las cuales se realizan las visuales de nivelación.
• Línea horizontal: Es toda línea contenida en el plano horizontal, siendo tangente a la respectiva línea y tiene la misma dirección.
• Línea vertical: Es la línea recta bajada hacia el centro de la tierra, lo cual corresponde a la dirección de la gravedad en dicho punto. Dentro de los límites topográficos se puede considerar como el hilo de una plomada que pende sobre el punto.

Métodos altimétricos

Los métodos altimétricos, llamados también métodos de nivelación, tienen como finalidad la determinación del desnivel entre dos o más puntos.

En altimetría se utilizan tres métodos para el cálculo de los desniveles que se denominan:

• Nivelación geométrica
• Nivelación trigonométrica
• Nivelación barométrica.

El método más exacto de nivelación es por medio de la nivelación geométrica, el cual se fundamenta en la obtención del desnivel por medio de visuales obligadamente horizontales, utilizando para ello los niveles y las miras. Este método de nivelación, por su exactitud, constituye el método más apropiado para establecer puntos de cotas fijas (PCF) y para otros trabajos de elevada precisión, tales como el replanteo de sistema de riego y drenaje y de las obras de fábrica requeridas por éstos.

El método de nivelación trigonométrica le sigue en importancia al de nivelación geométrica y se fundamenta el desnivel por medio de visuales inclinadas se realizan con un teodolito taquímetro situado sobre uno de los puntos, a la m ira que se colocará sobre el otro punto, determinando con esta operación la lectura de los tres hilos del retículo (hilo superior, medio e inferior) que se proyectan sobre la m ira, así como el ángulo vertical (α) debido a la inclinación del anteojo con respecto a su posición horizontal.

La nivelación barométrica se fundamenta en la variación que experimenta la presión atmosférica debido a la diferencia de altitud de los puntos que se consideren. Por lo que puede deducirse el desnivel basándonos en la diferencia de presión que registra un barómetro cuando nos situamos sobre dicho punto. Este método es incierto por los desniveles, las variaciones meteorológicas y la densidad del aire no es constante. Su aplicación se limita a reconocimientos en zonas montañosas y exploraciones

Métodos generales de nivelación

• Nivelación por alturas o geométricas: Es el principal y más exacto, se verifica por medio de la diferencia de las distancias de dos puntos a un plano horizontal.

• Nivelación trigonométrica: Consiste en determinar las diferencias de altura entre dos puntos, por medio de los elementos que se usan en trigonometría como ángulos y distancias en el triángulo.

Nivelación Geométrica.

En la nivelación directa, se está midiendo directamente distancias verticales entre diferentes puntos de interés del terreno. Es el método más preciso para determinar diferencias de nivel y uno de los más usados.

Imagínese una mesa y una silla en un piso a nivel como se muestra en la Figura. 

Si se pudiera mantener un nivel de burbuja a la altura del nivel del ojo, 1,50 m  por ejemplo, y se extendiera imaginariamente el plano horizontal del nivel de burbuja por encima de la mesa, el plano cortaría una regla que estuviera verticalmente sobre la mesa a la altura de 0,75 m.

La diferencia de nivel entre la tabla de la mesa y el asiento de la silla sería de una distancia vertical de 1,050 –0,75 = 0,30 m.

En la nivelación práctica, la regla se sustituye por una mira de nivelación, y el nivel de burbuja se cambia por un instrumento topográfico llamado precisamente nivel. El nivel consiste esencialmente en un nivel de burbuja fijado a un anteojo que a su vez está montado en un trípode. Si la mesa y la silla se reemplazan por dos puntos sobre la superficie de la tierra, la sencilla ilustración de la figura 2 se convierte en un trabajo de nivelación real como se ve en la figura. 

Se ve que la altura del punto A sobre el plano de referencia es 1,500 – 0,750 = 0,75 m en tanto que la altura de C es 1,50 – 1,050 = 0,450 m sobre el plano de referencia. El plano de referencia es en este caso un plano imaginario que pasa por la parte superior de la estaca B.

Toda nivelación que se haga en un emplazamiento de construcciones y sea necesario referir al cero oficial, debe enlazarse con algún punto fijo PF o mejor aún a un vértice geodésico del SGM de acuerdo con las indicaciones que disponga en la carta topográfica del SGM de acuerdo con la zona donde se realiza la construcción.-  Los PF y vértices geodésicos se identifican en las referidas cartas topográficas y pueden localizarse en el terreno por sus emplazamientos de mojones de hormigón y/o material.

  Nivelación entre dos puntos

Para encontrar la diferencia de nivel entre dos puntos cualesquiera del terreno se utilizan un nivel y una mira.  En la siguiente figura , tenemos dos puntos  A y B distantes unos 120 metros y se desea conocer la diferencia de niveles o distancia vertical entre ambos puntos.  El nivel se coloca aproximadamente en el centro entre los puntos, se cala la burbuja con precisión para asegurar la horizontalidad de la línea de colimación. Se toma una primera lectura de mira mantenida verticalmente en A. Sea 2,500 m esta lectura, luego de lo cual se coloca la mira en B, y se toma la lectura 0,500.  

 Por el dibujo es claro que el punto B está mas alto que el A en  2,500 – 0,500 = 2,000 m.  Es decir que, la diferencia de lecturas en la mira es igual a la distancia vertical entre los puntos visados.

Ahora bien, si la cota del punto A es 95,400 , la altura del plano colimador sería de  95,40 + 2,50 = 97,90, y la cota del punto B resulta entonces  97,90 – 0,50 = 97,40 m.

Las ecuaciones de la nivelación geométrica aplicada en la teoría básica de la nivelación compuesta, son las siguientes:

Cota 1 + Latrás 1 = HPC

 

HPC – Ladelante = Cota 2       Estas dos ecuaciones elementales se repiten una y otra vez.-

 

En efecto, la COTA + L atrás = HPC    y     la cota de los puntos desde una posición del nivel es  Ci = HPC – Lint    o   Ci = HPC – Ladel.   Estas son las fórmulas básicas de la nivelación geométrica.

Debemos definir las expresiones L atrás, Lint,  Ladel. 

La lectura atrás (Latr) se define como la primera lectura realizada a un punto cuya cota es conocida o arbitrada, es la primera lectura realizada al posicionar un nivel.

Lectura intermedia (Lint) es la lectura realizada a un punto cuya cota deseo determinar desde una posición del nivel.  Lectura adelante (Ladel) es una lectura realizada a un punto cuya cota deseo determinar desde una posición del nivel, pero es la última que realizo antes de cambiar de posición el nivel y es la que da origen al punto de cambio. Es decir que los puntos de cambio son puntos leídos desde dos posiciones del nivel y permiten enlazar una nivelación simple con otra.  

Vemos el siguiente ejemplo de una nivelación compuesta con puntos de cambio (PC). Es decir, que cuando el campo de visual se entorpece, ya sea por la topografía abrupta que no permite visualizar la mira o por obstáculos(árboles, edificios), o simplemente por la distancia existente entre los puntos de interés a nivelar, es necesario cambiar de posición el nivel. Entonces el conjunto de nivelaciones simple encadenadas, referidas a una superficie de referencia única forma la nivelación compuesta. 

 

En este caso los puntos de cambio están señalizados con X e Y. Abajo se muestra la rutina de toma de datos de la nivelación geométrica en forma tabular, donde cada fila es un punto del terreno y las columnas a qué tipo de lectura corresponde y en la extrema derecha el valor objetivo de la nivelación, la elevación o cota de los puntos.

 

Punto	L atrás	L inte	Ladel	HPC	Elevación
A	4,200				21,32
X	4.150		0,700
Y	2,500		0,560
B			3,700

 

Como norma, al realizar el trabajo de campo identificaremos los puntos de cambio como PC 1 , PC2  ........PCn   de acuerdo con la cantidad de los mismos que tengamos en nuestro proceso de nivelación geométrica.-

Como prueba de asimilación del conocimiento, complete el   lector las cotas de los puntos de cambio X,  e  Y  y finalmente del punto B.

Finalizado dicho cálculo, tenga en cuenta que se puede verificar la bondad de su cálculo por una simple prueba, donde   L atrás –   Ladel =  Diferencia de cotas

 Métodos utilizados en la Nivelación Trigonométrica.

Primero tenemos los instrumentos utilizados se le llaman taquímetros, siendo el más perfeccionado es el teodolito-taquímetro que es necesario procesar en el gabinete los tomados en el campo para calcular la distancia horizontal y el desnivel que facilitan los trabajos.

En la nivelación trigonométrica se utilizan relaciones trigonométricas para establecer las distancias verticales entre puntos del terreno.

La diferencia de nivel o elevación entre dos puntos puede determinarse midiendo: a) la distancia inclinada (S)  u horizontal (H) entre los puntos, y b) el ángulo cenital (Z) o el ángulo vertical    entre los puntos. Así, en la figura de abajo si se miden la distancia inclinada S y el ángulo cenital Z  o el ángulo vertical  entre C y D,   la diferencia de nivel V  entre C y D   será  .    

 

V = S cos Z        o bien    V = S sin 

Esquema de la Nivelación Trigonométrica con estación total .-

 

pero la elevación del punto B donde se coloca el estadal(mira) o el prisma de una estación total será

_B = C_A + hi + V - P_sm

 

Cuando las distancias son muy grandes (S ≥ 500m) se debe introducir el término de corrección por curvatura y refracción, situación que se presenta modernamente con el trabajo con Estaciones totales, también se presentaba con el distanciómetro EDM montado sobre la alidada del teodolito.

Estrictamente, cuando uno trabaja con una estación total, aplica la corrección por curvatura y refracción permanentemente para todas las mediciones con su software de cálculo de elevaciones del terreno cualquiera fuere la distancia al punto visado. Obviamente nadie en su sano juicio va a tomar polares a puntos a distancias mayores al kilómetro al realizar nivelaciones trigonométricas a pesar de aplicar correcciones por la significación de su valor altimétrico, lo recomendable es no superar los 1300 metros como máximo.

Ejemplo de aplicación de las fórmulas de nivelación. De acuerdo con el croquis de nivelación geométrica compuesta, confeccionar la planilla de cálculo y verificar la bondad de los mismos. 

Esquema de apunte de lecturas en la mira, al realizar una nivelación geométrica compuesta. Prepare una planilla y resuelva la elevación de B, sabiendo que la elevación de A=27.32

 

La solución del problema planteado se encuentra en la planilla a continuación:

 

Punto	L atras	Linte	Ladel	HPC	Cota
A	0.763			28.083	27.32
PC1	0.954		1.145	27.892	26.938
PC2	1.363		2.018	27.237	25.874
PC3	2.716		1.727	28.226	25.510
PC4	1.233		1.124	28.335	27.102
B			1.322		27.013
∑	7.029		7.336

 

La diferencia de Latrás –Ladelante = -.307 indicando el signo que la cota desciende y es igual a 27.32-27.03 = 0.307, lo cual es la prueba de cálculo que verifica la correcta aplicación de las fórmulas de la nivelación

• Método de diferencia o diferencial o Método de desniveles

A la mira de espalda tomada en A se le resta algebraicamente la mira de frente en el punto B. Si la diferencia o desnivel es positiva, el punto B estará más alto que el punto A y para obtener la cota de B habrá que sumar a la cota del punto A el valor del desnivel.

• Método de la cota de instrumentos

La mira de espalda tomada en el punto A se suma a la cota de dicho punto obteniéndose, de esa manera, la altura a la que se encuentra el eje de colimación del instrumento con respecto a la superficie de referencia. Si a la altura del eje de colimación del instrumento, o simplemente cota de instrumento (CI), le restamos la mira de frente tomada en el punto B obtenemos la cota de dicho punto B.

Para hallar las cotas por el método de los desniveles procederemos del siguiente modo:

• Punto B ∆ Z = 1,327 – 0,723 = +6,04 m, o sea, el punto B estará más alto que el punto A.

• Cota de B = cota de A + ∆ Z = 107,265 + 0,604= 107,869 m.

• Punto C ∆ Z = 1,327 – 2,715 = - 1,388 m

El punto C estará más bajo que el punto A:

• Cota de C cota de A - ∆ Z =107,265 – 1,388 = 105,877 m.

• Punto D = ∆ Z = 1,327 – 2,934 = - 1,607m

El punto D estará más bajo que el punto A.

• Cota D = 107,265 -1,607 = 105,658 m.

• Punto E: ∆ Z = 1,327 – 1,028 = + 0,299 m

El punto E estará más alto que el punto A:

• Cota de E = 107,265 +0,299 = 107,564 m

Para hallar las cotas por el método de la cota del instrumento procederemos del siguiente modo:

• CI = cota de A + ME……. 107,265 + 1,327 = 108,592 m

• Cota de B = CI – MFB……108,592 – 0,723 = 107,869 m

• Cota de C = CI – MFC……108,592 – 2,715 = 105,877 m

• Cota de D = CI – MFD……108,592 – 2,934 = 105,658 m

• Cota de E = CI – MFE…….108,592 – 1,028 = 107,564 m

Levantamiento topográfico por nivelación diferencial de una poligonal abierta y quebrada

Efecto de la Curvatura Terrestre en la Nivelación

Considerando la Tierra como una esfera perfecta, una línea de nivel deberá estar en todos sus puntos equidistante del centro de la esfera. El nivel genera una visual horizontal que es tangente a la línea de nivel que pasa por el centro óptico del instrumento. Si se tuviera una mira en B, la lectura desde A sería por tanto demasiado grande, en la magnitud BB₁. Esta magnitud   es la corrección por curvatura c, y puede calcularse como sigue.

En el triángulo AB₁O,  L es la longitud de la visual y  R el radio promedio de la Tierra. Por el teorema de Pitágoras

(R + c)²  = R²  +  L²

 

esto es,  R² + 2 Rc + c²  =  R² + L²  ,  de donde   c(c +  2R) = L²

 c = L²  / (c +2 R )

 

Como  c  es muy pequeño en comparación con el radio de la tierra R, podemos despreciarlo y entonces  

c = L²  / (2 R )

asumiendo el valor 6378 km para el radio de la tierra

c = L²  / (12756 )

como c se necesita en metros y L seguimos midiéndolo en kilómetros

 c =  L²   x 1000/ (12756 )  metros

c = 0,0784 L²   m (con L en km)

En realidad la línea de visual tampoco es estrictamente horizontal, porque la afecta la refracción atmosférica en forma que se curva hacia abajo. A pesar de que no es un valor constante, se acepta que tiene un valor de 1/7 del de curvatura, por lo cual el efecto combinado de curvatura y refracción se calcula como:

Corrección combinada = 0,0784 L² -  (1/7) 0,0784 L²

                                     =  6 / 7 (0,0784 L²)  

                                     =  0,0672 L²     m  (con L en km)

 

En conclusión,  el error por curvatura terrestre y refracción (Error_CR) de una visual horizontal es directamente proporcional a la longitud de la misma y responde a la fórmula  siguiente :

Error _CR  (m) =  0,0672  L²

 

tomando la distancia  L en kilómetros, asumiendo un radio de la Tierra de 6.378 km, valor que coincide con cualquier modelo terrestre. 

 

ErrorCR	L (km)
0.003 m	0.2
0.011 m	0.4
0.017 m	0.5
0.067 m	1.0
1.075 m	4.0

La técnica de la nivelación geométrica no tiene necesidad de corregir por curvatura sus mediciones, porque se realiza en forma tal que el operador se desplaza por el terreno con el nivel manteniendo distancias de visadas no superiores a 200 - 250 metros y la curvatura se toma en cuenta “per se”.  Ahora en cambio, con la nivelación trigonométrica que es la base de la taquimetría con la Estación Total, es necesario tener en cuenta el efecto de la curvatura y refracción y corregir las mediciones para compensar aquellos efectos. 

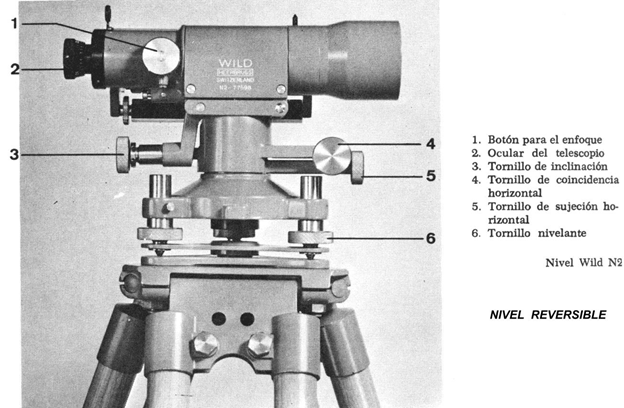
  Instrumentos utilizados en la Nivelación Geométrica y su aplicación

Niveles

Llamados también equialtímetros o niveles fijos, son los instrumentos que se utilizan para la nivelación geométrica, es decir, para determinar el desnivel que existe entre dos puntos por medio de una visual horizontal.

Una vez situado el nivel, en condiciones de trabajo, deberá lograrse que las visuales que por él se dirijan, sean obligadamente horizontales; y de acuerdo con las distintas maneras de lograr esta condición.

Los niveles se clasifican en:

• Niveles planos: Son aquellos instrumentos en los cuales el eje vertical es perpendicular al eje de colimación una vez estacionados.

• Niveles de línea: El eje de colimación puede experimentar ligeras inclinaciones respecto al eje vertical de giro, ya que aun así podemos situar perfectamente horizontal el eje de colimación de cada visual. Estos son los de mayor uso en la actualidad.

• Niveles automáticos: Como su nombre lo indica queda automáticamente horizontal la visual, su inconveniente es el mayor costo y su reparación.

Nivel de ingeniería de alta precisión

Miras

Instrumento que se usa en todos los procesos, pero en altimetría la menor división es el centímetro, y en el caso de tener que usar el milímetro debe ser estimado por el instrumentista. Existen diferentes miras de acuerdo a la operación a realizar y su precisión.

Videos de como se hace una nivelación de un terreno usando el nivel fijo y estadía

Parte I

Parte II

PERFILES TOPOGRAFICOS

Perfiles. 

Una de las aplicaciones más usuales de la nivelación geométrica es la obtención de perfiles del terreno, a lo largo de una obra de ingeniería o en una dirección dada. Las obras hidráulicas como canales o acueductos y las vías de comunicación y transporte, como caminos y ferrocarriles, están formados por una serie de trazos rectos y curvas acodadas a los trazos rectos. Generalmente la sección transversal de las obras mencionadas, posee un eje de simetría, que no varía de tipo a lo largo del trazado. Los diversos tipos de perfiles que se levantan tienen por objeto representar la forma y las dimensiones del terreno en la zona de proyecto.

Perfil Longitudinal.

Se llama perfil longitudinal a la intersección del terreno con un plano vertical que contiene al eje longitudinal y nos sirve para representar la forma altimétrica del terreno. Los puntos del terreno por levantar quedan definidos durante el estacado del eje del proyecto, por lo cual, la distancia horizontal acumulada desde el origen del kilometraje es un dato conocido, que esta materializado en terreno, próximo a cada estacado. Se llama estacado, a un conjunto de señales o estacas clavadas para indicar la posición deleje del trazado, las que se colocan generalmente a distancias o intervalos iguales dependiendo de la naturaleza de la obra. La determinación de las cotas del estacado se hace mediante una nivelación geométrica, ligada y cerrada contra el sistema altimétrico de transporte de cota.

Nivelación de un Perfil Longitudinal.

El levantamiento del perfil longitudinal en terreno corresponde a una nivelación geométrica de todas las estacas que lo conforman, llevando a un registro las lecturas que se observen conjuntamente con la distancia acumulada a cada punto. El registro que conviene emplear es del tipo “Por Cota Instrumental”. Antes de iniciar la nivelación geométrica del perfil longitudinal se debe establecer, a lo largo del estacado y a una distancia conveniente de él, puntos de referencia de cota conocida (P.R.). Estos puntos de referencia se ubicarán, no tan distantes del eje de   referencia del trazado como para que las medidas importen trabajo excesivo, ni tan cercanos como para que se vean comprometidos por el movimiento de tierras o labores auxiliares de la construcción de la obra. En todo caso su ubicación debe efectuarse sobre terreno estable y serán debidamente monumenticos.

Perfiles Transversales de Terreno y Perfil Tipo.

El perfil transversal es la intersección del terreno con un plano vertical perpendicular al eje longitudinal y nos sirve para tomar la forma altimétrica del terreno a lo largo de una franja de nivelación. El perfil transversal tiene por objeto presentar, la posición que tendrá la obra proyectada (perfil tipo) respecto del terreno y a partir de esta información, determinar la cubicación del movimiento de tierra, ya sea en forma gráfica o analítica. El perfil tipo representa las características finales que tendrá el proyecto. En el caso de un proyecto vial se consideran ancho de la pista, el bombeo, ancho bermas y su pendiente, los taludes, espesor de las capas estructurales etc. El perfil tipo es variable dentro del proyecto, debido que los parámetros antes mencionados pueden cambiar según las condiciones impuestas por la topografía, climatología y/o geología de la zona. A continuación, se muestran algunos ejemplos de perfiles tipos: La siguiente figura representa un perfil tipo para un camino bidireccional, los taludes se encuentran en la relación 3/2 en corte y 2/3 en terraplén, el valor depende del tipo de suelo que se encuentre en la zona, así por ejemplo para la roca el talud de corte es 1/10.

 

 

La pista, la berma y sus bombeos respectivos, dependen de la funcionalidad del camino, el tipo de vehículo y de las condiciones climáticas de la zona. Los espesores de las capas estructurales dependen del tipo de vehículo que circule por el camino.

Este representa el perfil tipo para un carretero unidireccional, se pueden apreciar taludes de corte en banco, cunetas, fajas, etc. 

Se aprecia un perfil tipo para un túnel, donde indican sus dimensiones y las capas estructurales. 

 Procedimiento para levantamiento de perfiles transversales.

Para efectuar el levantamiento de perfiles transversales se procederá de la siguiente manera:

•        Definición del Perfil Transversal: En cada estaca del perfil longitudinal, se debe definir un eje transversal en la forma más perfecta posible. Se puede recurrir a medidas con cinta métrica o escuadras, que permitan asegurar su perpendicularidad. El eje transversal así definido se puede señalar, mientras dure su levantamiento, con estacas u otro elemento de instalación provisoria.

•        Levantamiento de los Puntos Singulares: Para la confección del perfil transversal se deben tomar todos los puntos que definan o ayuden a definir cambios de pendientes del terreno, cruce de canales, cercos, y cualquier otro detalle de interés o punto singular. Recorriendo el eje longitudinal en el sentido creciente del kilometraje, las distancias horizontales sobre los ejes transversales que se miden hacia la derecha serán positivas y las que se midan a su izquierda serán negativas, ambas con su origen en el eje longitudinal.

Las distancias horizontales se miden con cinta métrica y precisión corriente (cuidando su horizontalidad, etc.). En casos de fuerte pendiente se puede calcular midiendo la distancia inclinada entre los puntos y el desnivel, para posteriormente aplicar Pitágoras.

 Con un nivel de ingeniero se realizan las lecturas en la mira, se registran al centímetro y se refieren al sistema altimétrico del levantamiento, ya sea apoyándose en P.R. o en estacas de perfil longitudinal.

 En casos de pendientes fuertes o en túneles el desnivel se puede establecer trigonométricamente o por medio de instrumentos que midan por rebote, tales como las estaciones totales.Pendiente de una Línea: Se define como la tangente del ángulo formado con la horizontal, la cual se puede expresar tanto en grados como en porcentaje.

Es el grado de inclinación de la línea que une dos puntos de un terreno.  Se denota con la letra m. 

La pendiente se calcula como la relación entre el desnivel y la distancia horizontal.  El resultado de esta relación se puede notar en tanto por uno o en tanto por ciento.

Los registros deben consignar, para cada punto del perfil, la distancia horizontal y los datos para determinar la cota. Si la medición es indirecta se debe agregar las columnas de los elementos que efectivamente se miden para calcular las distancias horizontales y verticales. 

Dibujo de perfiles Longitudinales y Transversales. 

Para dibujar perfiles longitudinales se utilizan dos escalas, una horizontal y otra vertical, la relación entre ellas debe ser 1/10, es decir la escala vertical es 10 veces mayor que la horizontal, por ejemplo, si la escala horizontal es 1/1000, la vertical será 1/100.

La figura anterior representa parte de un perfil longitudinal la distancia entre las estacas es de20 metros y la cota de referencia (C.R) es de 220 metros, la longitud del perfil es de 240 metros. 

Para dibujar las distancias deben ser transformadas al papel utilizando la escala horizontal1/1000, es decir, 20 metros de terreno representa en el papel 2 centímetros o 20 milímetros. Para dibujar las cotas restar la cota de referencia y transformar el valor resultante utilizando la escala 1/100, los datos dibujados se anotan en la viñeta según se muestra en la figura

Una de las principales utilidades del perfil longitudinal es permitir el trazado de la rasante (línea segmentada en la figura anterior), que corresponde a un conjunto de líneas y/o curvas que definen la posición altimétrica y pendientes finales del camino sobre el terreno. Existen varios criterios para trazar la rasante sobre el perfil longitudinal, los que van en directa relación con las especificaciones del proyecto. El caso del un camino se deben considerar los siguientes:

• La rasante debe compensar los volúmenes de corte y terraplén.
• Las pendiente deben estar comprendidas entre un ±10%, valor que puede variar dependiendo del tipo de vehículo y la velocidad de proyecto del camino.
• Se deben evitar las pendientes iguales a 0%, porque causan problemas de drenaje.

Aplicaciones de los perfiles topográficos

Los perfiles topográficos tiene una enorme cantidad de aplicaciones, ya que son muy usados en muchos ámbitos de la vida. Eso sí, sin duda alguna, sus aplicaciones más importantes tienen que ver con todo lo relacionado con la construcción.

Por ejemplo, este tipo de perfiles son muy usados en obras de gran longitud como puede ser la construcción de carreteras, de redes de alcantarillado y oleoductos.

También los geólogos, edafólogos o geomorfólogos les dan un gran uso a los perfiles topográficos para el estudio de recursos naturales o de vegetación. Por ejemplo, hacen uso de los perfiles para poder estudiar la relación de los recursos naturales con los cambios de topografía y con ellos realizar diferentes análisis que les puedan proporcionar información de interés.

Cómo elaborar un perfil topográfico

• Escoge dos puntos del mapa, de los que puedas conocer su altitud a partir de las curvas de nivel o bien porque esté indicada su altitud. Llámalos A y B respectivamente.
• Une ambos puntos A y B.
  

• Marca los puntos por donde pasan las curvas de nivel. Esto lo puedes hacer sobre el mapa, o bien si no quieres estropear este, puedes usar una hoja auxiliar.
• Una vez hechas las marcas de las curvas de nivel debemos de llevarlas a un gráfico, tal y como puedes ver en la imagen;
• El gráfico estará compuesto por dos ejes, X e Y, en el que irá representada la altitud en la unidad que hayas escogido, o más bien en la unidad que nos hemos encontrado en el mapa con el que hemos empezado a trabajar. Ahora solo se trata de ir situando en el gráfico la altitud de cada curva de nivel y unir todos los puntos obtenidos para tener listo nuestro perfil topográfico.

VIDEOS DE COMO HACER PERFILES TOPOGRAFICOS A MANO O EN AUTOCAD

Como dibujar PERFIL LONGITUDINAL a MANO

DIBUJO DE SECCIÓN TRANSVERSAL

Dibujando un perfil topográfico

DIBUJO DE UN PERFIL DE TERRENO EN AutoCAD